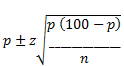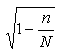Beregn den statistiske usikkerhed for en andel, når du generaliserer fra stikprøvens konkrete svar til populationens formodede svar.
Eksempel på indtastning
24 procent af 1050 adspurgte skolelærere mener, at elevers brug af mobiltelefoner i undervisningen er en berigelse for undervisningen.
- Tast 24 i “andelens størrelse”
- Tast 1050 i “antal svar i stikprøven”
- Lad feltet population stå tomt
- Vælg 95% konfidensniveau
Sådan fortolker du resultatet
Den statistiske usikkerhed i eksemplet med skolelærere er +- 2,6 procentpoint. Vi kan derfor med 95% sikkerhed sige, at mellem 21,4 og 26,6 procent af danske skolelærere mener, at elevers brug af mobiltelefoner i undervisningen er en berigelse for undervisningen.
Note: Der er meget større sandsynlighed for, at den sande værdi (her: danske skolelæreres holdning) ligger centralt i konfidensintervallet end i intervallets yderpunkter (her: 21,4 og 26,6).
Anbefalinger
Konfidensniveau: Vi anbefaler, at du vælger et 95 procent konfidensniveau. Med dette niveau har man ret 19 ud af 20 gange i sine forudsigelser, og det anses normalt som tilstrækkeligt – også i videnskabeligt arbejde.
Populationens størrelse: En fjerde ting, som kan have betydning for usikkerheden, er forholdet mellem stikprøvens størrelse og populationen. Du kan indtaste populationens størrelse i beregneren – så tages der automatisk højde for dette forhold. Vi anbefaler dog, at du kun gør det, hvis stikprøven udgør en væsentlig del af populationen (50% eller mere). I de mange tilfælde, hvor stikprøven udgør mindre end 50%, lader du blot feltet ”population” stå tomt.
Disclaimer
Beregneren er ikke velegnet til at beregne konfidensintervaller for andele meget tæt på 0% og 100%. Og den kan faktisk slet ikke beregne intervaller for andele på præcist 0% og 100% (prøv gerne selv at sætte disse værdier ind). Der findes andre metoder (baseret på andre statistiske modeller) til at beregne konfidensintervaller for en andel. Nogle af dem (fx Clopper-Pearson) håndterer bedre andele tæt på eller lig 0% og 100%. Tjek fx sammenligningen af 5 forskellige metoder her. Vi har valgt den metode, man typisk bruger i samfundsvidenskaberne. Fælles for metoderne er dog – betryggende nok – at de fører til konfidensintervaller, som ligger meget tæt på hinanden.
Matematikken bag
Her er formlen for beregning af konfidensintervallet:
p: andelens størrelse (i eksemplet er p = 24)
z: konfidensniveauet (ved 95 % er z-scoren = 1,96)
n: stikprøvens størrelse (i eksemplet er n = 1050)
Den endelige korrektionsfaktor, som kan ganges på det beregnede konfidensinterval, hvis man ønsker at korrigere konfidensintervallet for forholdet mellem stikprøve og population:
n: stikprøvens størrelse (i eksemplet er n = 1050)
N: populationen (i eksemplet er N uoplyst)