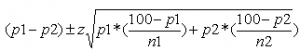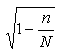Beregn om forskellen på to andele er statistisk signifikant, når du generaliserer fra stikprøvernes konkrete svar til populationens formodede svar.

Eksempel på indtastning

I en måling mener 35 procent af 980 adspurgte danskere, at Danmark bør tilslutte sig euroen.
I en ny måling et halvt år senere mener 42 procent af 1020 adspurgte danskere, at Danmark bør tilslutte sig euroen. Er den øgede tilslutning fra første til anden måling statistisk signifikant? Kan man konkludere, at tilslutningen blandt danskerne faktisk er øget? Og i givet fald med hvor meget?

• Tast 35 i andel 1
• Tast 980 i stikprøve 1
• Lad feltet population 1 stå tomt
• Tast 42 i andel 2
• Tast 1020 i stikprøve 2
• Lad feltet population 2 stå tomt
• Vælg 95% konfidensniveau

Sådan fortolker du resultatet

Konfidensintervallet for forskellen på de to andele går fra 2,7 til 11,3 i eksemplet med spørgsmålet om tilslutning til euroen. Vi kan derfor med 95% sikkerhed sige, at tilslutningen til euroen hos den samlede danske befolkning fra den første til den seneste måling er steget med mellem 2,7 og 11,3 procentpoint. Stigningen er derfor statistisk signifikant.
Note: Der er meget større sandsynlighed for, at den sande forskel i danskernes tilslutning til euroen ligger centralt i konfidensintervallet end i intervallets yderpunkter (her: 2,7 og 11,3).

Anbefalinger

Konfidensniveau: Vi anbefaler, at du vælger et 95 procent konfidensniveau. Med dette niveau har man ret 19 ud af 20 gange i sine forudsigelser, og det anses normalt som tilstrækkeligt – også i videnskabeligt arbejde.

Populationens størrelse: En fjerde ting, som kan have betydning for usikkerheden, er forholdet mellem stikprøvens størrelse og populationen. Du kan indtaste populationens størrelse i beregneren – så tages der automatisk højde for dette forhold. Vi anbefaler dog, at du kun gør det, hvis stikprøverne udgør en væsentlig del af populationen (50% eller mere). I de mange tilfælde, hvor stikprøverne udgør mindre end 50%, lader du blot feltet ”population” stå tomt.

Matematikken bag